반응형
직선을 제외한 곡선 함수는 평면에서 위로 볼록하거나, 아래로 볼록하거나 둘 중 하나입니다.
그런데 보통 문제에서 f(x)는 어느 구간에서 위로 볼록하다- 이런식으로 주지 않거든요.
이걸 수식으로 어떻게 나타내는지 오늘 살펴볼 거에요.

1. 고1 수학 : 내분점과 함숫값의 내분점을 비교. (주로 중점을 사용)
| 아래로 볼록 | 위로 볼록 |
곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 |
곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여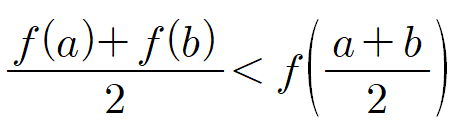 |
 |
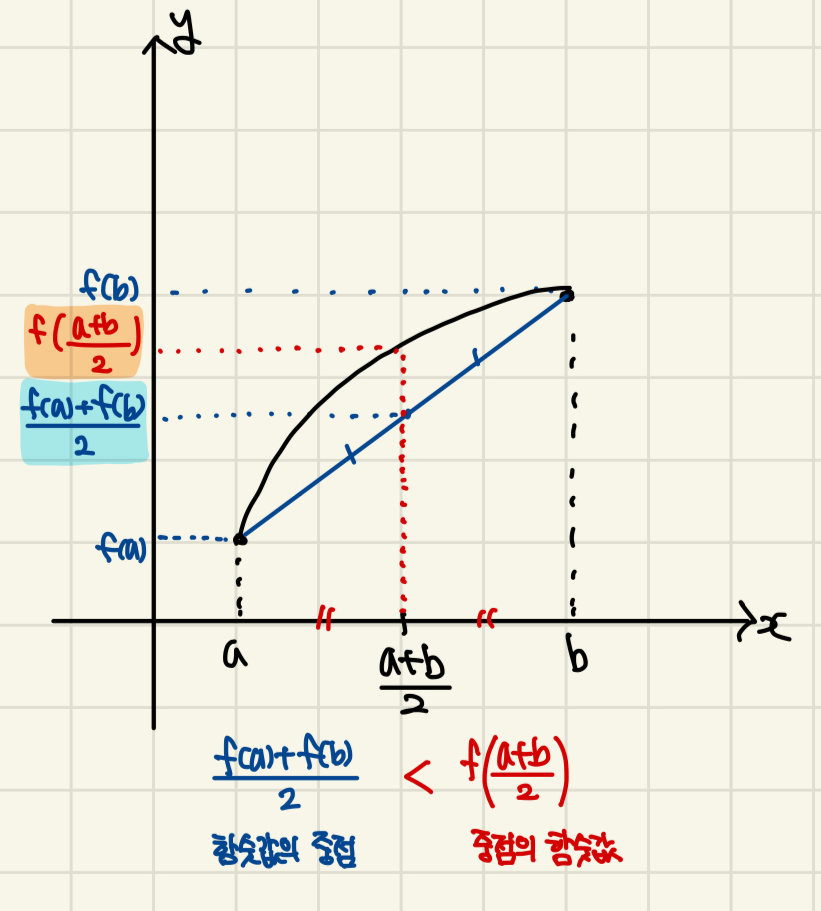 |
만약 아래와 같이 함숫값의 중점과 중점의 함숫값이 항상 같다고 나온다면?

이건 직선을 의미한답니다 :-)
2. 수학2
① 두 평균변화율을 비교하여 판정
| 아래로 볼록 | 위로 볼록 |
| 곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)), C(c, (c)) (단, a<b<c)에 대하여  |
곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) C(c, (c)) (단, a<b<c)에 대하여  |
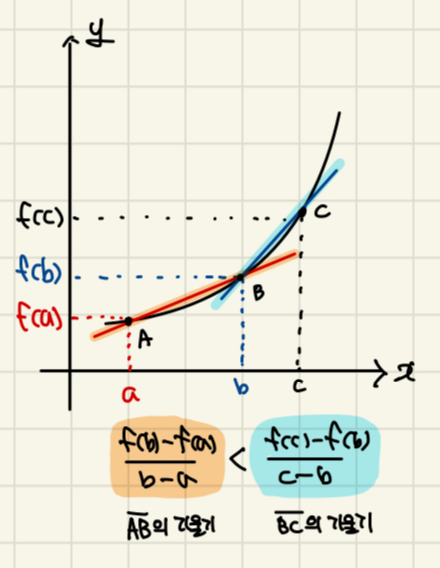 |
 |
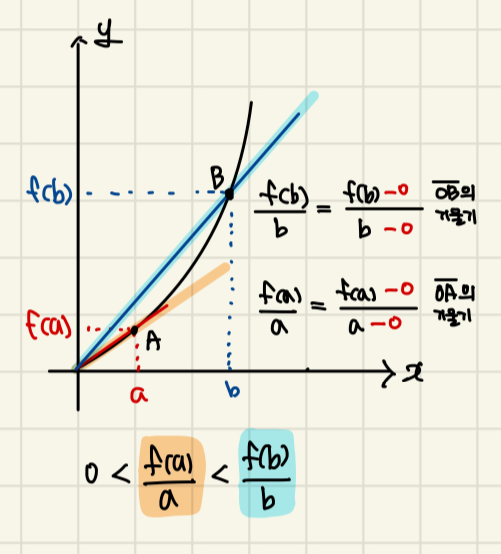
② 원점과 곡선 위의 점을 지나는 직선의 기울기를 이용한 방법
| 아래로 볼록 | 위로 볼록 |
| 원점을 지나는 다항함수 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단,0< a<b)에 대하여 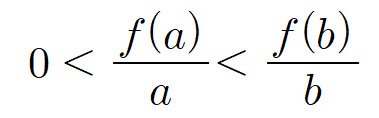 |
원점을 지나는 다항함수 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단,0< a<b)에 대하여  |
| 0<bf(a)<af(b) | bf(a)>af(b)>0 |
 |
 |
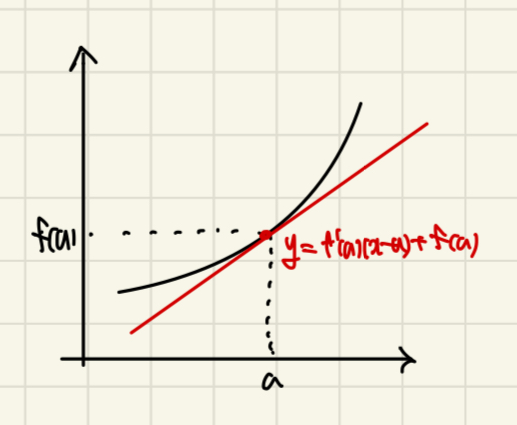
③ 접선의 방정식과 함수의 그래프를 이용한 방법
| 아래로 볼록 | 위로 볼록 |
| x=a에서의 접선이 곡선 y=f(x)의 아래쪽에 있다. | x=a에서의 접선이 곡선 y=f(x)의 위쪽에 있다. |
| f(x) ≥ f'(a)(x-a)+f(a) | f(x) ≤ f'(a)(x-a)+f(a) |
 |
 |
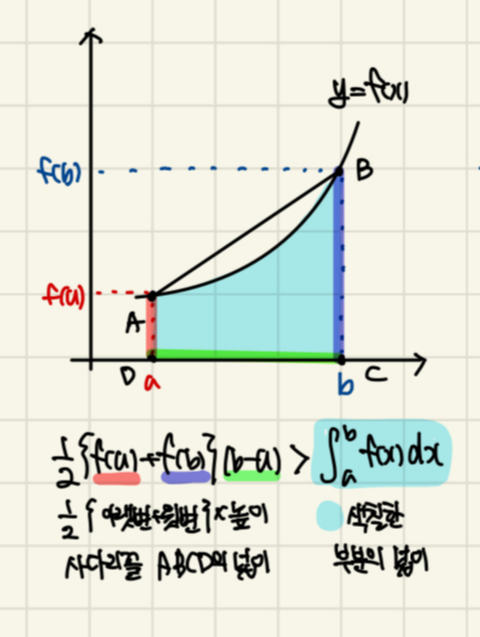
④ 정적분과 사다리꼴의 넓이를 비교하여 판정하는 방법
| 아래로 볼록 | 위로 볼록 |
| 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 | 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 |
 |
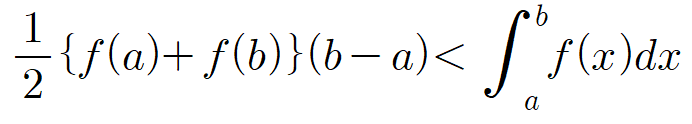 |
 |
 |
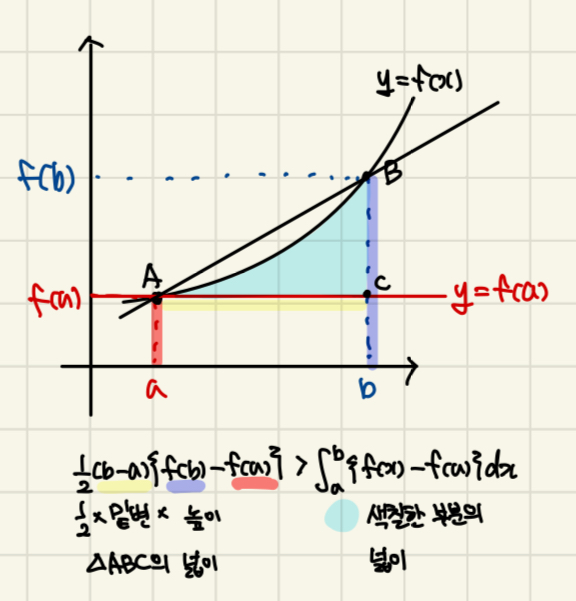
⑤ 정적분과 삼각형의 넓이를 비교하여 판정하는 방법
| 아래로 볼록 | 위로 볼록 |
| 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 | 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 |
 |
 |
 |
 |
미적분까지 배우시면 이계도함수의 부호를 이용하는 방법도 추가 된답니다.
고1때까지만 하더라도 중점을 이용한 방법만 주로 다루는데, 수학2를 배우고나면 함수의 개형을 나타내는 방법이 매우 다양해집니다. 연습을 다양히 해보도록 하세요!
반응형
'고등수학 (2015 개정 교육과정) > 수학2' 카테고리의 다른 글
| 적분 속도 문제 모음 (0) | 2023.12.02 |
|---|---|
| [삼차함수] 서로 다른 세 실근 => 극대x극소로 푸는 문제 (0) | 2023.11.10 |
| 삼차함수 접선의 개수 문제 모음 (0) | 2023.08.27 |
| [수학2] 가우스 들어있는 극한 문제 유형별 정리 (0) | 2023.08.20 |
| 내신 대비 - 평균값 정리 선별 문제 (0) | 2023.05.28 |