중3 내신에서 사용할 수 있는 유용한 꿀팁을 하나 알려 드리겠습니다.
증명 다 한 다음, 예제 풀고 정리해드릴테니,
여러분은 이해한 다음 공식을 외워서
빠르고 편하게 문제를 풀면 되겠죠?

아래 그림과 같이 두 원 P, Q는 서로 외접하고 동시에 지름의 길이가 R인 반원 O에 내접합니다. 접하는 세 원들의 반지름 길이비를 구해볼게요.

원끼리 반지름이 반, 반의반.. 뭐 이렇게 간다고 외우셔도 됩니다.
이제 증명 해볼게요.
원P의 지름 = 원O의 반지름이므로,
비율이 2:1이 되는 것은 쉽게 알 수 있습니다.

작은원 Q의 반지름을 r, 큰 원 O의 반지름을 R이라고 두고, 중심끼리 연결한 보조선과 접선에 내린 수선의 발을 같이 그려줍니다. 이 과정은 원을 보면 항상 해봐야 하죠.

그리고 가장 큰 원 O의 중심과 가장 작은 원 Q의 중심도 연결해줍니다. 그림에서 보이는 빨간 형광펜 선이죠.

원 안에 다 그리자니 복잡하군요. 그래서 삼각형 POQ만 따로 모양을 관찰하려고 아래와 같이 가져 왔습니다.
Q에서 선분 PO에 수선의 발을 내리면 각각 노란색, 빨간색 직각삼각형이 나오니, 이 둘의 공통변을 이용하여 식을 정리해줍니다.

결론 : 큰 원의 반지름 R = 가장 작은 원 반지름 r의 4배

이제 문제를 풀어볼까요?
예제
아래 그림과 같이 두 원 P, Q는 서로 외접하고 동시에 지름의 길이가 20인 반원 O에 내접한다. 이 때 원Q의 둘레의 길이를 구하여라.
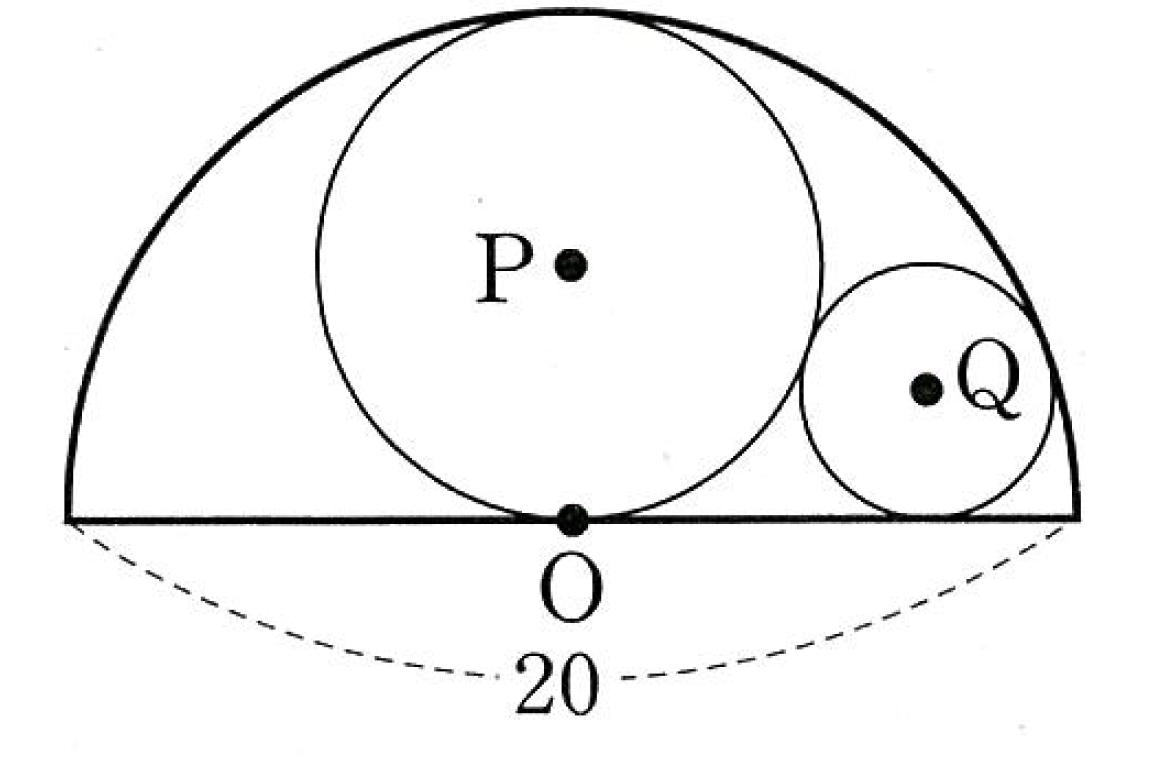
정답 : Q의 반지름은 5/2이므로 둘레의 길이는 5π
다음에도 좋은 꿀팁 있으면 갖고 오겠습니다 :-)
'중등수학 > 중등 3학년' 카테고리의 다른 글
| 통계 - 분산 제평평제 (제곱의 평균)-(평균의 제곱) 연습문제 (0) | 2024.11.11 |
|---|---|
| [중3 통계] 분산 (제곱의 평균) - (평균의 제곱) 증명 및 활용법 (0) | 2024.11.08 |
| 중3 삼각비 - 넓이로 푸는 문제 모음 (2) | 2024.09.29 |
| 근호가 있는 식 - 소숫점 옮기는 유형에서 다른 숫자가 나오는 경우 (1) | 2024.04.24 |
| [삼각비] 특수각 사인, 코사인, 탄젠트 15º, 75º, 22.5º, 67.5º (0) | 2022.09.17 |