최단거리 문제는 살짝만 바꿔도 조금씩 달라지므로 최대한 다양한 문제를 풀어서 연습하는 것이 중요합니다.

예제1.
아래 그림과 같은 도로망이 있을 때, A지점에서 출발하여 B까지 최단거리로 가는 방법의 수를 세어라.

최단거리 문제는 항상 최단 방향을 먼저 파악한 다음 푸셔야 합니다. 그리고 지날 수 없단 조건이 나온다면, 지날 수 있는 길만 남겨두고 세는 게 더 좋겠죠?
sol1) 같은 것이 있는 순열로 풀이

sol2) 직접 세기

예제2
아래 그림과 같은 도로망이 있다. 색칠한 부분은 공사 중이어서 지나갈 수 없을 때, A지점에서 B 지점까지 최단거리로 가는 방법의 수를 구하여라. (단, 모든 도로는 평행하거나 수직으로 만난다.)

우선은 최단거리 방향을 파악합니다. 그리고 지날 수 없는 길은 버립시다.

도식을 조금 더 간단하게 만든 다음 세면 됩니다.
sol1) 대각선 방향으로 지점 나눠서 같은 것이 있는 순열로 세기

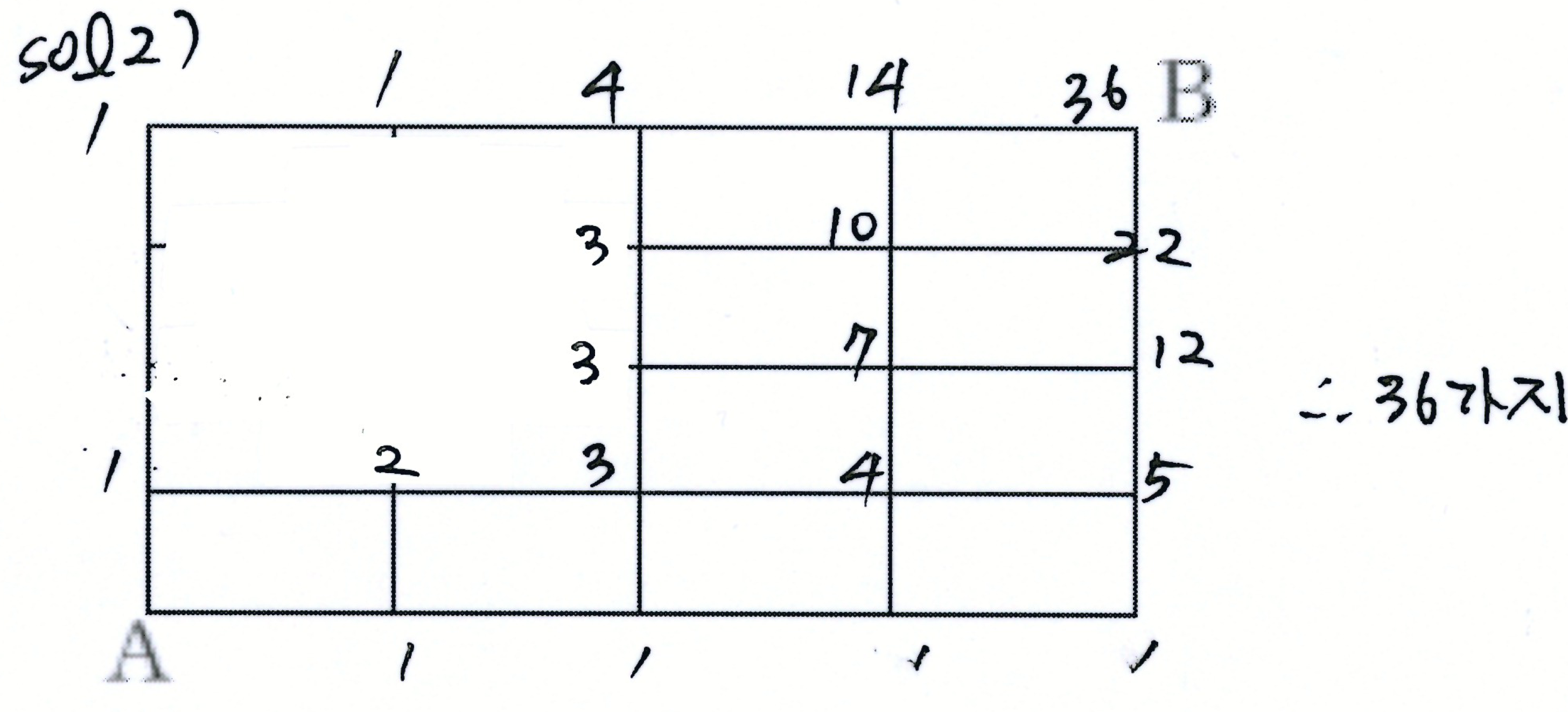
sol2) 직접 세기
예제3
아래 그림과 같은 도로망이 있을 때, A 지점에서 출발하여 B지점까지 도로망을 따라 최단거리로 가는 방법의 수는?
(단, 모든 도로는 평행하거나 수직으로 만난다.)

sol1) 최단거리에 해당하는 도로만 파악한 다음 세기

이 경우 대각선을 그어서 세도 상관없습니다. 지점 세 개 잡고 세면 되겠네요 :-)
sol2) 여사건을 이용해서 세도 됩니다.

예제4
어느 부대가 그림과 같은 바둑판 모양의 도로망에서 장애물(어두운 부분)을 피해 A지점에서 B지점으로 도로를 따라 이동하려고 한다. A지점에서 출발하여 B지점까지 최단 거리로 가는 경우의 수를 구하여라.
(2017 사관학교 기출)


역시나 장애물은 지나갈 수 없는 경로이므로, 갈 수 있는 부분만 표시해서 생각해봅시다.
sol1) 최단거리
최단방향 파악하여 대각선으로 선을 그어보면 지점이 몇 개 안 나오기 때문에 금방 셀 수 있습니다.

sol2) 직접 세기

예제5
아래 그림과 같이 직사각형 모양으로 연결된 도로망의 가운데 호수가 있다. A지점에서 B지점 까지 도로를 따라 최단 거리로 가는 경우의 수는?
(2012년 7월 교육청 기출)

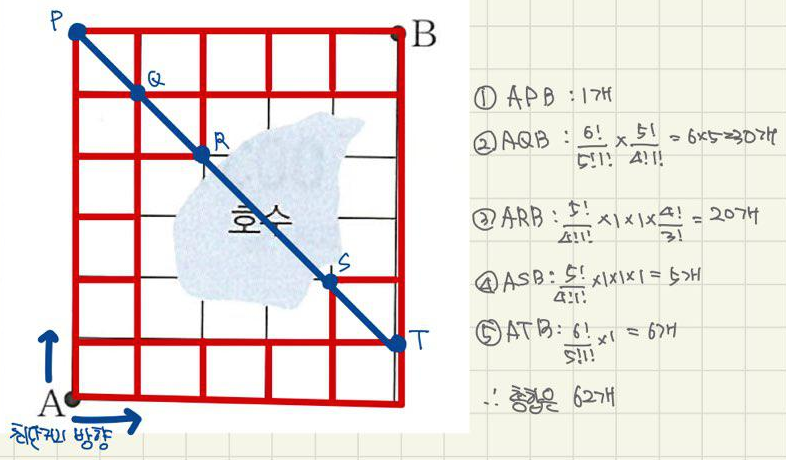
sol1) 직접 세기


sol2) 대각선으로 지점 나눠서 세기
최단거리 문제는 다양한 문제들을 접해보는 게 중요합니다. 어떤 풀이가 좋을지가 문제마다 다르기 때문이죠. 위의 문제가 수월하게 풀린다면 아래 포스팅에 실린 문제들도 도전해보시기 바랍니다!
https://ladyang86.tistory.com/134
[경우의 수] 최단경로 문제풀이#2 (실력정석)
최단거리 경우의 수 이 부분이 유형이 다양한데 문제지마다 다 실려있는 게 아니라, 문제풀이 포스팅을 몇 번 더 해볼까 합니다. 가장 기초적인 문제는 아래의 포스팅으로 먼저 풀어보시고, 이
ladyang86.tistory.com
조금 더 난도가 있는 어려운 문제들도 다음에 이어서 포스팅 할테니 기대해주세요^^
'고등수학 (2015 개정 교육과정) > 확률과 통계' 카테고리의 다른 글
| [이항정리] 이항계수의 성질 - 제곱꼴 (0) | 2021.01.17 |
|---|---|
| [원순열] 정다면체 색칠하는 경우의 수 (5가지 모두 같은 방법으로 다룸) (0) | 2021.01.10 |
| [중복조합] 부정방정식의 정수해 조건 부분 (0) | 2020.11.18 |
| 배수 판정법 (초중고딩 모두 이해할 수 있음) (0) | 2020.11.05 |
| [조건부 확률] 독립이 되는 사건 쉽게 찾기 (0) | 2020.09.26 |