반응형
명제에서 집합의 포함관계를 이용하여 필요충분조건을 판별하는 문제가 있길래 갖고 와봤습니다.
벤다이어그램을 이용하여 풀면 금방 풀리는데, 그냥 증명하려면 좀 힘들거 같더라고요.!
오늘 예제로 갖고 온 건 한 문제지만, 나중에 더 발견하게 되면 추가하겠습니다.
문제
세 집합 A,B,C에서 두 조건 p,q가 다음과 같을 때, p가 q이기 위한 필요충분조건인 것을 찾으시오.
(가)
p : A∩(B∩C)=A
q : A∪(B∪C)=B∩C
(나)
p : A∪(B∩C)=A
q : A∩(B∪C)=B∪C
(다)
p : A∪(B-A)=B
q : A ⊂ B
문제를 풀 때 p가 무슨 조건인지 모두 찾아보세요.
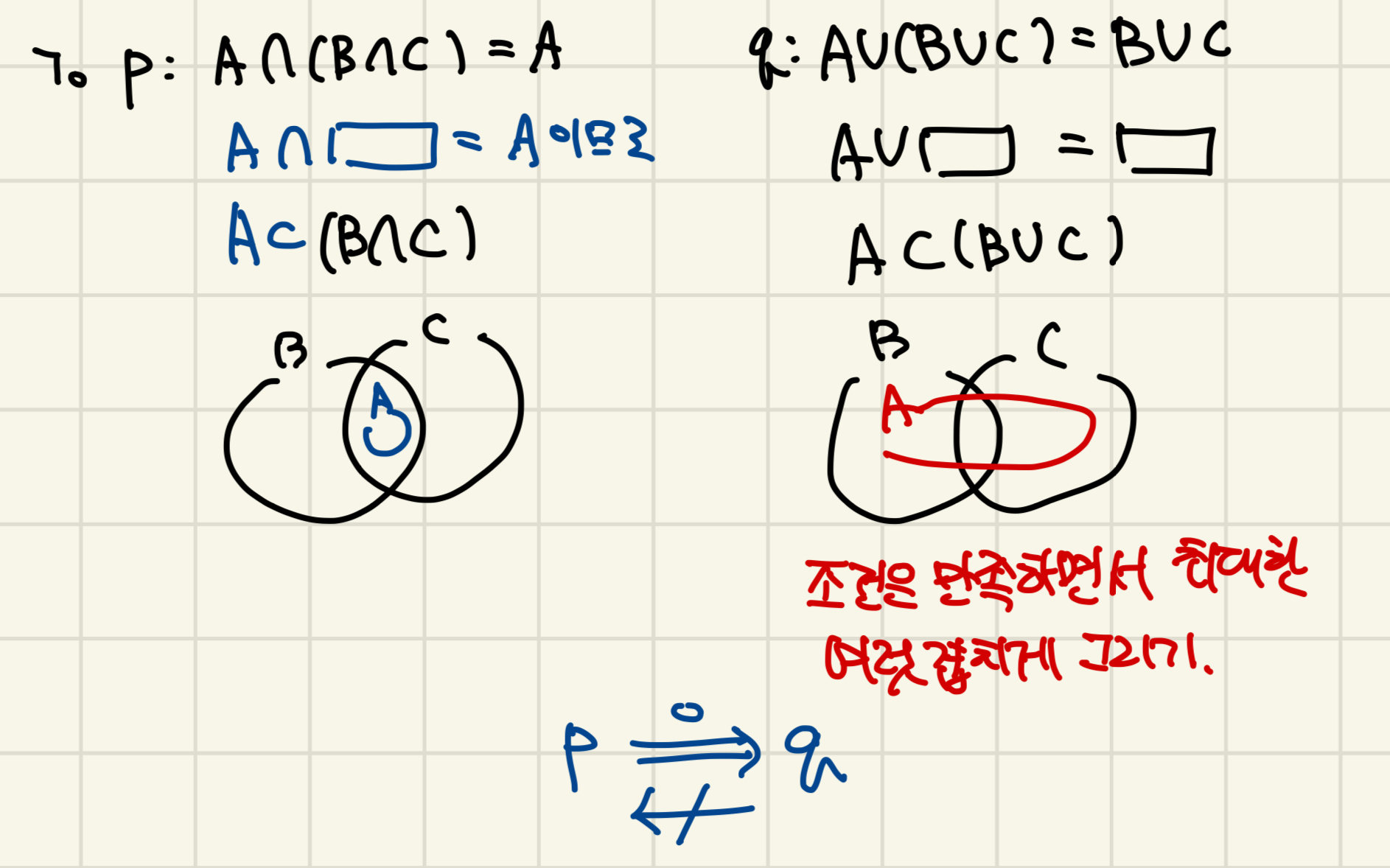


집합의 포함관계의 경우 저는 주로 벤다이어그램을 그려서 찾는 편인데 이게 익숙해지면 굉장히 편하답니다. :-)
조건에 맞는 벤다이어그램을 그려본 다음 p이면 q가 되는지 확인을 해보시면 되겠죠?
반응형
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| 일차함수의 역함수 y= f(ax+b)의 역함수 구하기 (0) | 2024.12.15 |
|---|---|
| [집합] 대칭차집합의 여집합 성질 정리 (0) | 2024.11.15 |
| 무리함수의 그래프와 직선의 위치 관계 - 반드시 그래프 그려야 하는 이유 (1) | 2024.11.13 |
| [고1 함수] 일반적으로 정의된 함수 문제 (0) | 2024.11.09 |
| [집합] 약수, 배수 들어가는 문제 정리 (0) | 2023.10.08 |