오늘은 알아두면 매우 강력한
내용을 배워볼까 합니다.
보통은 원의 방정식에서
가장 학습하기 어려워 하는 부분이
접선의 방정식입니다.
이 중에서도 극선에 관한 내용을 살펴볼거에요.

극선이 뭔가요?
원 밖의 점에서 원에 그은 접선은 항상 2개입니다.
그러니 접점도 항상 2개죠.
이 두 접점을 이은 직선을 극선이라고 합니다.
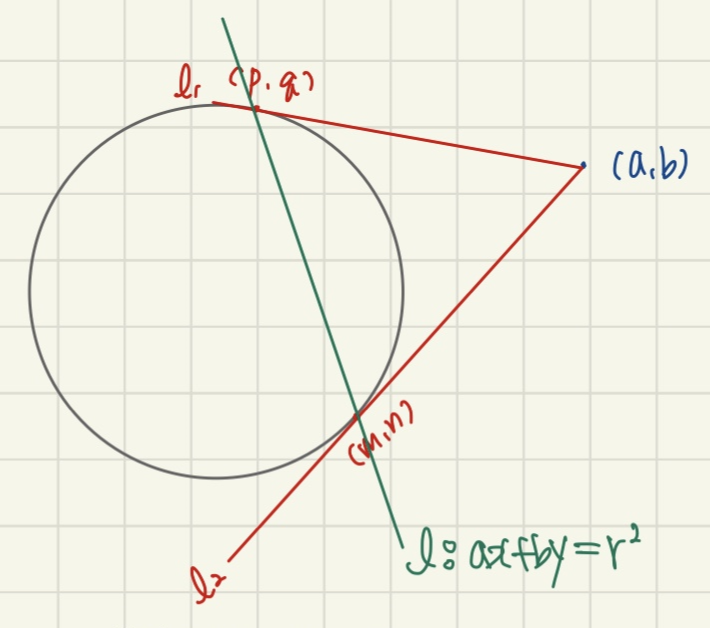
그러니까 l이 극선인 거죠!
극선의 방정식 구하는 법
* 아래의 모든 증명을 가시성을 높이기 위해
일부러 좌표를 서로 다른 문자로 썼습니다.
일반적인 교재에서는 해당 점을 모두
(x1, y1), (x2, y2)와 같이 표기하고 있으니
염두하고 보세요.
<증명>
(a,b)에서 원에 그은 두 접선을 l1, l2라고 합시다.
원 위의 점에서 그은 직선의 방정식은
쉽게 구할 수 있으므로
l1과 l2를 각각 구해줍니다.

두 직선이 모두 원 밖의 점 (a,b)를 지나죠.
즉 (a,b)가 직선 위의 점이므로
식에 대입해도 성립합니다.

여기서 두 일차식을 살펴보면,
a,b,지름이 공통이네요.
이 계수를 살려서
일차식 한 번 만든 후 관찰을 해봅시다.

아니 이것은..!!


방금 구한 직선이 두 접점을 지나네요!
즉, 두 접점을 지나는 직선인
극선의 방정식이 구해졌습니다.

쓰고보니 이 식이 되게 익숙하죠?
원 위의 점에서 그은 접선의 방정식과
생김새가 거의 비슷하기 때문에 그렇습니다.

해당 점이 원 밖인지, 원 위인지
잘 판단하셔야겠죠?
예제1
중심이 (0,0)이고 반지름이 10인
원 위의 점 (6,8)에서의 접선의 방정식
vs
중심이 (0,0)이고 반지름이 4인
원 밖의 점 (6,8)에서 원에 그은
두 접점을 지나는 직선의 방정식

꼭 원점일 때만 가능한가요?
No!
원 위의 접점과 동일합니다.
어차피 평행이동 한 것이니
원리는 동일합니다.
예제2
중심이 (1,2)이고 반지름이 2인 원
밖의 점 (10,3)에서 원에 그은
두 접선의 접점을 지나는
극선의 방정식을 구해보죠.
(x-1)(x-1) + (y-2)(y-2)=4로
식을 풀어준 다음,
(10,3)을 하나씩 대입하면
(10-1)(x-1)+(3-2)(y-2)=4입니다.
정리하면 9x+y=15가 됩니다.
참 쉽죠?
그럼 다음에도 쉽고 유용한 포스팅으로
찾아올게요!

'고등수학 > 고등수학(상)' 카테고리의 다른 글
| 길이비를 내/외분점으로 고치는 방법 (선분의 내분점,외분점 활용) (0) | 2022.01.02 |
|---|---|
| 원 위의 점에서의 접선 빨리 구하는 팁! (2) | 2021.09.02 |
| 삼차방정식 f(ax+b)=0의 근에 관한 문제 (합,곱 쉽게 풀기) (0) | 2021.06.11 |
| 삼차방정식 - 역수를 근으로 갖는 방정식 외 기타 (0) | 2021.05.31 |
| 계수가 대칭인 상반방정식 (대칭형 사차방정식) 푸는 방법 (0) | 2021.05.08 |