경우의 수와 확률을 가리지않고
이웃하지 않게 나열하는 방법을
탐구해볼까 합니다!
이건 사실 수학(하) 순열과 조합부터
확률과 통계까지 다 나오기 때문에
꼭 알고 있어야 하는 내용이에요.

우선, 이웃하게 나열하는 건,
① 이웃해야 하는 걸 한 그룹으로 묶고,
② 전체 나열 & 이웃 내부 그룹 나열
이렇게 하는 거 아시죠?ㅎㅎ
이웃하지 않는건 이것과 조금 다릅니다.
① 이웃해도 상관없는 걸 먼저 나열하고,
② 방금 나열한 것 사이사이에
이웃하지 않아야 하는 걸 배열하면 됩니다.
아래에 다양한 예제와 함께
문제를 풀어가면서 감을 익히도록 해보죠!
예제1.
남자 5명, 여자3명을 일렬로 나열할 때,
여자 3명이 누구도 이웃하지 않는
경우의 수를 구하여라.
① 우선 이웃해도 상관없는
남자 5명을 먼저 나열합니다.
5!=120

② 남자 사이사이의 6개의 자리중
3자리를 골라서

여자 3명을 나열하면 됩니다.

이 부분은 따로 구분하여
6C3 x 3! 로 보셔도 되고,
그냥 6P3으로 계산해도 무관합니다.
어쨌건
전체 경우의 수는 120x120=14,400이죠.
예제2.
서로 같은 빈의자 8개에
ABC가 앉으려고 한다.
누구도 이웃하지 않게 앉는
경우의 수를 구하여라.

의자가 8개 있는데,
사람이 앉을 의자는 3개이므로
나머지 5개는 빈 의자가 됩니다.
① 우선 이웃해도 상관없는
빈 의자 5개를 먼저 나열합니다.

이 때 빈 의자는 모두 같기 때문에
나열하는 경우의 수는 1가지입니다.
② 빈 의자 사이사이의 공간 6곳 중,
(v로 표시된 부분)
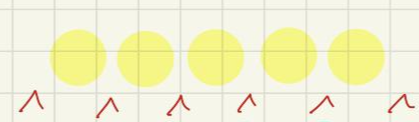
사람이 들어갈 3자리를 고른 다음,
6C3 = 20개
ABC를 앉힙니다.
3!=6개
전체 경우의 수는 20x6=120개입니다.
예제 2의 빈의자 알고리즘은
순서가 정해져있는 경우에도
동일하게 사용합니다.
예제3.
2019년 7월 학평 나형 #16
어느 수영장에 1번부터 8번까지
8개의 레인이 있다.
3명의 학생이 서로 다른 레인의 번호를
각각 1개씩 선택할 때,
3명의 학생이 선택한 레인의 세 번호 중
어느 두 번호도 연속되지 않도록
선택하는 경우의 수는?
숫자가 1부터 8까지 있지만,
위의 빈 의자 8개 모델을
그대로 적용해보겠습니다.
처음부터 서로 이웃하지 않게
숫자를 고르는 것은 힘들기 때문이죠.
그냥 숫자가 안써진 8개의 레일에
사람 ABC를 이웃하지 않게
나열을 할 거에요.
다 나열한 다음 맨 마지막에
레일 번호를 붙여줄거랍니다.

그럼 이것도 사람이 없는 빈 레일 5개와
사람이 서 있을 레일 3개를 나열하면 돼요!
① 사람이 서 있을 레일은 이웃하면 안되니까,
이웃해도 상관없는
서로 같은 빈 레일 5개를 나열합니다.

이 때 빈 레일은 모두 같기 때문에
나열하는 경우의 수는 1가지입니다.
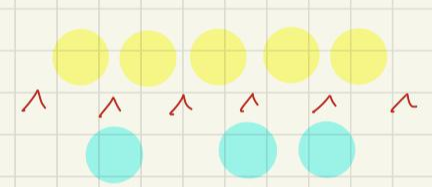
② 빈 레일 사이사이의 공간 6곳 중,
(v로 표시된 부분)

사람이 서 있을 3자리를 고른 다음,

6C3 = 20개

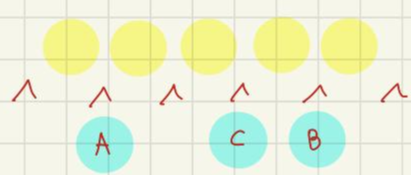
ABC를 배열합니다.
3!=6개
전체 경우의 수는 20x6=120개네요.
읭? 저희 숫자 써진 레일에
사람 나열하는 문제였잖아요?

자, 이제 최종적으로 앞에서부터
숫자를 써주시면 됩니다.
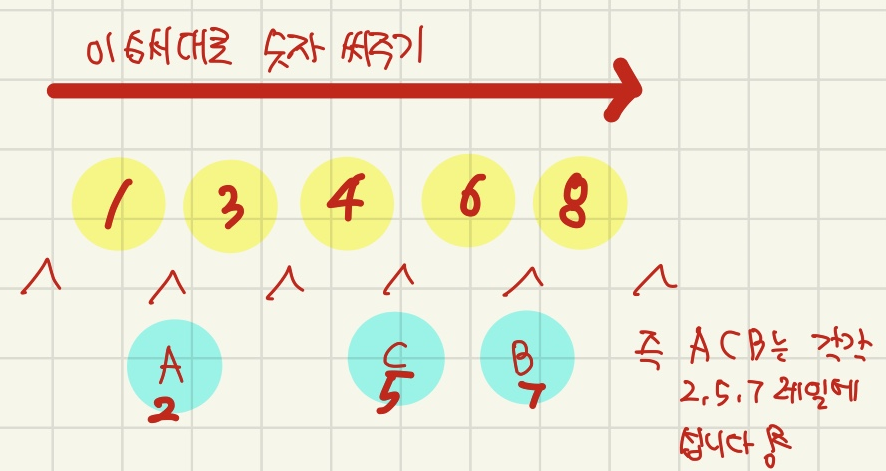
사실 빈 의자에 이웃하지 않게 사람을 앉히는 것과
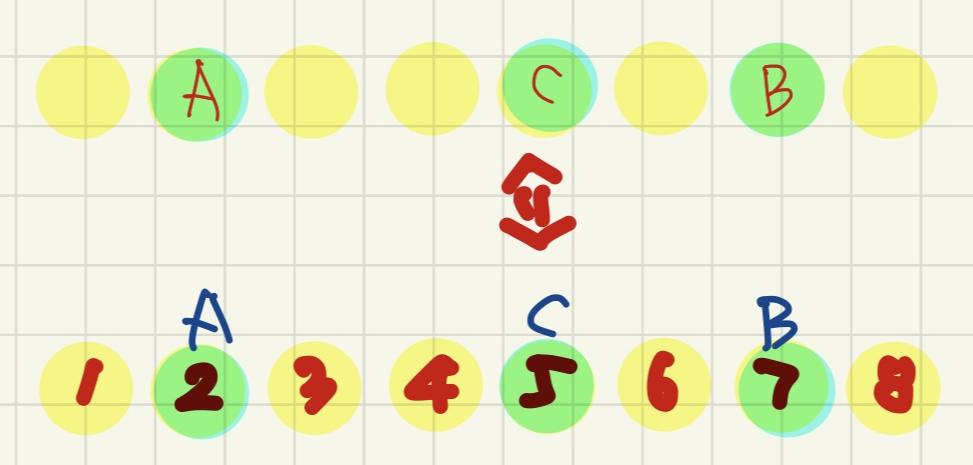
1~8번까지의 레일 중,
이웃하지 않게 3명을 배열하는 것은
일대일 대응이 됩니다.
즉 한쪽을 정하면,
나머지 하나도 똑같이 정할 수 있죠.
일대일 대응은 서로 개수가 같기 때문에,
세기 편한 모델로 세면 됩니다.
예제4
2020년도 6월 모평 가형 #19

이 문제는 먼저 정리를 좀 해봅시다.
(가) 조건에 n=1,2,3을 차례로 대입하면
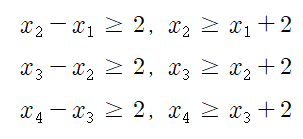
즉, 우리가 정해야 하는 4개의 문자는
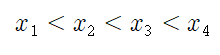
대소관계가 정해져 있습니다.
그리고 같은 숫자가 될 수 없는데다
연속해서 숫자를 고를수도 없습니다.

그러니까, 다시 문제를 이해해보자면
0부터 12까지의 정수 중
이웃하지 않는 4개의 정수를 고르는
방법의 수를 물어보는 겁니다.
그냥 4개의 정수를 고르고
작은 순서대로 넘버링 하면 되는거죠!
이것도 빈 의자 문제로 바꿔봅시다.
의자가 총 13개 있습니다.
(0부터 12까지 총 13개)
ㅇㅇㅇㅇㅇㅇㅇㅇㅇㅇㅇㅇㅇ
이 중 4개를 고를거에요.
그럼 선택이 된 의자 4개와
선택되지 않은 의자 9개가 있겠죠?
① 선택할 의자 4개는 이웃하면 안되니,
빈 의자 9개를 먼저 나열해줍니다.
의자는 같으니까 경우의 수는 1입니다.
② 빈 의자 사이사이의 10개의 공간 중
vㅇvㅇvㅇvㅇvㅇvㅇvㅇvㅇvㅇv
4개를 골라줍니다.
10C4=210
따라서 구하는 경우의 수는 210개입니다.
처음부터 숫자를 붙이면 끝!
예를 들어
vㅇㅇvㅇㅇㅇㅇvㅇㅇvㅇ
이렇게 선택하면
차례대로 (0,3,8,11)로
매핑이 됩니다.
예제5
2020년도 6월 모평 나형 #29

위의 문제와 동일합니다.
(가) 조건에 n=1,2을 차례로 대입하면

즉, 우리가 정해야 하는 3개의 문자는
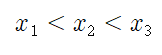
대소관계가 정해져 있습니다.
그리고 같은 숫자가 될 수 없는데다
연속해서 숫자를 고를수도 없습니다.

그러니까, 다시 문제를 이해해보자면
0부터 10까지의 정수 중
이웃하지 않는 3개의 정수를 고르는
방법의 수를 물어보는 겁니다.
그냥 3개의 정수를 고르고
작은 순서대로 넘버링 하면 되는거죠!
이것도 빈 의자 문제로 바꿔봅시다.
의자가 총 11개 있습니다.
(0부터 10까지 총 11개)
ㅇㅇㅇㅇㅇㅇㅇㅇㅇㅇㅇ
이 중 3개를 고를거에요.
그럼 선택이 된 의자 3개와
선택되지 않은 의자 8개가 있겠죠?
① 선택할 의자 3개는 이웃하면 안되니,
빈 의자 8개를 먼저 나열해줍니다.
의자는 같으니까 경우의 수는 1입니다.
② 빈 의자 사이사이의 9개의 공간 중
vㅇvㅇvㅇvㅇvㅇvㅇvㅇvㅇv
3개를 골라줍니다.
9C3=84
따라서 구하는 경우의 수는 84개입니다.
처음부터 숫자를 붙이면 끝!
예를 들어
ㅇㅇvㅇvㅇㅇㅇvㅇㅇ
이렇게 선택하면
차례대로 (2,4,8)로
매핑이 됩니다.
예제6
15개의 자리가 있는 일자형의 놀이기구에
5명이 타려고 할 때,
5명이 어느 누구와도 서로
이웃하지 않게 될 확률은?
우선 전체 경우의 수는 15개의 자리 중
5자리를 골라서 사람을 앉히는 것이므로
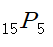
가지 입니다.

이제 원하는 사건을 구해봅시다.
15개의 자리 중,
사람이 앉을 자리는 5개,
빈자리 10개입니다.

① 이웃해도 상관없는 빈자리 10개를
먼저 나열해줍니다.
같은 자리이므로 경우의 수는1개이죠.
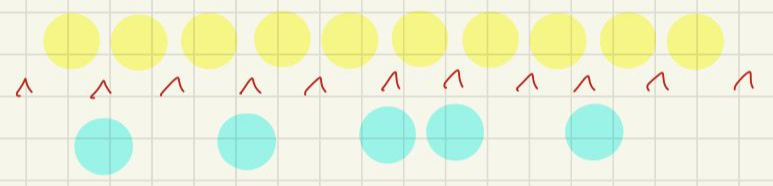
② 사이사이의 빈 자리 11개 중
사람이 앉을 5자리를 골라줍니다.
11C5
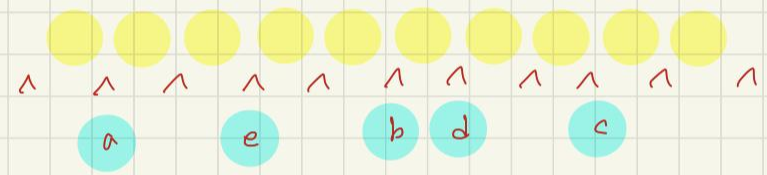
그리고 사람을 앉힙니다.
5!
사실 위 식에서 따로 썼지만,
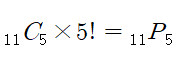
이므로 계산은 그냥 하시면 됩니다.
구하는 확률은
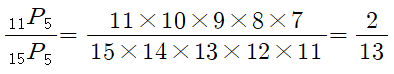
예제7
그림과 같이 회색과 검은색 서류철 10개를
일렬로 책꽂이에 남김없이 꽂으려고 한다.
검은색 서류철끼리는 서로 이웃하지 않고
양 끝에는 회색 서류철이 오도록 꽂는
경우의 수를 구하시오.
(단, 같은 색의 서류철은 서로 구별하지 않는다.)

검은색 서류철끼리 이웃하지 않아야 합니다.
① 이웃해도 되는 회색 서류철을 먼저
배치하는 방법은 한 개
ㅇㅇㅇㅇㅇㅇㅇ
② 회색 서류철 사이사이에
검은색 서류철을 끼우면 됩니다.
양 끝에는 회색 서류철이 들어가야 하므로,
검은색 서류철이 들어갈 수 있는 자리는
ㅇvㅇvㅇvㅇvㅇvㅇvㅇ
회색 서류철의 사이사이인
v자로 표기된 6개의 자리죠.
즉 6C3=20개 존재합니다.
예제8.
1부터 9까지의 자연수가 하나씩 적혀있는
9장의 카드가 있다.
이 카드 중에서 동시에 3장을 선택할 때,
카드에 적인 어느 두 수도
연속하지 않는 경우의 수를 구하여라.
역시나 위의 레일과 의자문제와 동일합니다.
빈 의자 9개에서
이웃하지 않게 3개를 선택하는 경우를
세면 됩니다.
즉, 선택되는 의자 3개 + 빈의자 6개인거죠.
① 이웃해도 상관없는 빈의자 6개를
먼저 일렬로 나열합니다.
ㅇㅇㅇㅇㅇㅇ
같은 의자이므로 경우의 수는 1개입니다.
② 빈 의자 사이사이의 7개의 공간 중
v o v o v o v o v o v o v
의자를 놓을 3자리를 선택합니다.
7C3=21개죠.
예를 들어
v o v o o o o v o라면
(1,3,8)을 고른것이죠.
예제9
집합 X={1,2,3,...,200}에서 50개의 원소를 가지는 부분집합 중에서 임의의 두 원소의 차가 3 이상인 부분집합의 개수를 nC52라 할 때, 자연수 n의 값을 구하시오. (단, n≥52인 자연수이다.)
풀이 : 모든 원소의 차가 3 이상이 되어야 한단 이야기는, 숫자와 숫자 사이에 2이상 띄워져있어야 한다는 말입니다. 즉, 의자 모델 적용시, 모든 숫자 사이에 적어도 의자가 2개 이상 들어있어야 한다고 풀면 됩니다.
정답 : 102
이웃하지 않는 알고리즘을 가르치다보면
항상
전체에서 이웃하는 거 빼면 안되나요?

-라는 질문을 받게 됩니다.
네. 안됩니다!
사실 두명일 땐 상관없는데,
셋 넘어가면 많이 힘들어요.
왜냐?
분명 전체에서 셋다 이웃하는 걸 뺄 텐데..
그럼 두 명만 이웃하는 게
안빠지기 때문이죠.
이걸 다 또 세서 빼느니,
그냥 처음부터 이웃하지 않는 방법을
익혀서 쓰시는 편이 낫습니다.
'고등수학 (2015 개정 교육과정) > 확률과 통계' 카테고리의 다른 글
| 서로 다른,같은 공을 상자에 넣는 문제 (0) | 2021.09.04 |
|---|---|
| 2021년 7월 학평(인천) 확통 30번 상세 해설 - 색별로 공 넣는 문제 (0) | 2021.08.28 |
| [이항정리] 이항계수의 성질 - 제곱꼴 (0) | 2021.01.17 |
| [원순열] 정다면체 색칠하는 경우의 수 (5가지 모두 같은 방법으로 다룸) (0) | 2021.01.10 |
| [경우의 수] 최단거리 문제풀이 #1 (기본문제) (0) | 2021.01.09 |